본문 바로가기

알고리즘7

[C++] BFS - 톰과 제리 풀이 일반적인 BFS와 다르게 단순 최단거리가 아닌, 방향을 최소한으로 바꾸는 횟수를 구해야 한다. 이때, 특이한 방법을 사용하는데 4방향에 대해서 while loop를 사용해 범위를 벗어나지 않거나, 벽이 아니거나, 이미 업데이트 되지 않은 위치라면 해당 위치를 업데이트 하는 것이다. 기존 BFS에서 1칸씩 이동하며 업데이트 했던 것과 달리, 한 방향에 대해 갈 수 있는 모든 위치를 한번에 업데이트 한다. 직진의 경우 방향이 바뀌지 않기 때문에 한번에 업데이트 할 수 있다. 또한, BFS이므로 채워지지 않은 영역에 도달하는 최소 방향 전환 횟수를 구할 수 있다. 단, 벽이 1로 표시되고 채워지지 않은 영역이 0이므로 벽과 방문지점을 구분하기 위해 시작점을 2로 하여 시작한다. 리뷰 처음에 한 지점에 대.. 2023. 2. 27.
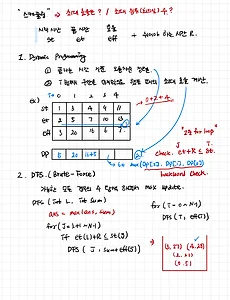
[Algorithm] 스케쥴링, Scheduling 백준 문제를 풀면서 스케쥴링과 관련된 알고리즘을 정리한다. 크게 DP, DFS, Stack를 활용한 문제가 있었다. 문제 유형은 최대 효율, 최대 동시 점유 수, 횟수 최소화 등 최적화(효율)와 관련된 문제들이다. https://www.acmicpc.net/problem/19598 19598번: 최소 회의실 개수 2개 회의실로 3개 회의를 모두 진행할 수 있다. 예를 들어, 첫번째 회의실에서 첫번째 회의를 진행하고 두번째 회의실에서 두번째 회의와 세번째 회의를 진행하면 된다. 1개 회의실로 3개 회의 www.acmicpc.net https://www.acmicpc.net/problem/1931 1931번: 회의실 배정 (1,4), (5,7), (8,11), (12,14) 를 이용할 수 있다. www.ac.. 2023. 2. 2.
[Algorithm] 다익스트라(Dijkstra) 1. 다이나믹 프로그래밍을 활용한 대표적인 최단경로 탐색 알고리즘 2. 가중치 그래프에서, 임의의 점에서 목표점까지의 최소 비용 거리를 탐색할 수 있다. 3. 현재 점과 연결된 노드 중, 가중치가 가장 작은 노드를 선택 방문하여, 시작점으로부터 그 점까지의 거리를 업데이트 한다. 4. 3번 과정을 반복하면서, 특정 노드를 직접 방문했을 때 보다, 다른 점을 거쳐서 왔을 때의 거리가 작다면, 그 거리를 업데이트 하게 된다. 우선순위 큐 사용 알고리즘 1. 가중치 그래프를 저장하기 위한 구조체와 우선순위 큐(최소 힙)를 선언한다. 벡터를 사용해 구현할 시, 최소 가중치 노드를 찾기 위한 for loop 가 필요한데, 최소힙을 사용하면 이 과정을 O(log N)으로 줄일 수 있다. 2. 우선순위 큐에 시작점을.. 2023. 1. 21.
[Algorithm] Minimum Spanning Tree - Prim 1. Prim 알고리즘은 최소 신장트리를 우선순위 큐를 통해 찾는다. 2. BFS 알고리즘에서 그래프 가중치가 존재하는 경우라고 보면 될 것 같고, 우선순위 큐를 사용한다는 점 이외에 알고리즘은 동일하다. 3. 최소 힙을 통해 가중치가 가장 작은 간선부터 탐색해 나가고, 각 노드를 방문했는지 체크하는 과정을 통해 싸이클을 막을 수 있다. #include #include #include #include using namespace std; /* 최소 신장 트리 (MST) 1. Kruscal 알고리즘: Union-find 알고리즘을 활용 2. Prim 알고리즘: priority-queue */ int ch[30]; struct Edge{ int e; int val; Edge(int a, int b){ e=a.. 2023. 1. 19.
[Algorithm] Minimum Spanning Tree - Kruscal 최소 신장 트리(MST)를 찾는 알고리즘으로 Union-Find 아이디어를 활용한다. Union-Find 란 disjoint set을 찾기 위한 아이디어 이다. 전반적인 아이디어는 다음과 같고, 알고리즘은 아래 코드에서 확인하면 된다. Union(a, b): a, b 노드가 연결되어 있다면 a 가 b를 연결시킨다. 즉, a = 1과 b=2가 연결되어 있다면 unf[a] = b 이다. 이때, unf[ ] 는 연결된 노드를 표시하기 위한 배열이고, 자기 자신을 가리키도록 초기화 된다. 즉, unf[1] = 1, unf[2]=2, unf[3]=3 .... unf[n]=n 이다. 1 과 2 노드를 Union 시키기 위해, 각 노드가 가리키는 루트노드를 찾는 Find(n) 재귀 함수를 실행한다. Find 재귀함수.. 2023. 1. 19.
[Algorithm] 연속된 자연수 합 풀이 자연수 n을 자기자신을 제외한 연속된 자연수의 합으로 표현할 수 있는 수식을 찾는 알고리즘. 15를 표현한다면, 7+8 = 15, 4+5+6 = 15, 1+2+3+4+5 = 15, 세 가지 수식으로 표현 가능하다. 이때, 2자리로 표현하는 경우는 (15 - (1+2)) / 2 = 6 (1+6) + (2+6) = 7+8 = 15 이다. 3자리는 (15 - (1+2+3)) / 3 = 3 (1+3) + (2+3) + (3+3) = 4+5+6 = 15 이다. 1부터 연속한 자연수의 합을 제외하고 남은 수를, 각 수에 동등하게 배분하여 해결할 수 있다. #include int main() { int a, b=1, cnt=0, tmp, i; scanf("%d", &a); tmp=a; // 1 빼기 a--; w.. 2023. 1. 16.
[Algorithm] Two-Pointer (투 포인터 알고리즘) 풀이 1. 두 집합의 교집합을 찾기 위한 알고리즘 2. 이중 for loop를 사용할 때는 O(N^2) 이지만, 투 포인터 알고리즘으로 O(N)으로 해결 가능 3. 각 집합을 오름차순 정렬하고, 두 포인터 변수가 가르키는 값이 다르다면 작은 쪽의 포인터를 증가, 같다면 모두 증가 시키는 방법으로 교집합을 찾는다 예시) a: {1 3 4 6} b: {4 5 6 7} 오름차순 정렬된 두 집합이 존재할 때 a 집합의 포인터를 p1 = 0, b 집합의 포인터를 p2=0 라 하자. a[p1] < b[p2] 이기 때문에 a 집합에서 더 큰 원소를 가져와서 비교해야 한다. 따라서 p1++ 한다. 계속 진행해서 p1 = 2 일 때 a[p1] == b[p2] 가 되고, 모든 포인터를 하나씩 증가시키면서 교집합을 업데이트.. 2023. 1. 16.

티스토리툴바